Sociala medier
Kategorier
- Allmänt
- Annat
- Event
- Custom bike show 2015
- Ferdinand Ice Festival 2014
- Motormässan 2014
- One Mile 2015
- Speed Weekend on Ice 2010
- Speed Weekend on Ice 2011
- Speed Weekend on Ice 2012
- Speed Weekend on Ice 2013
- Speed Weekend on Ice 2014
- Speed Weekend on Ice 2015
- Speed Weekend on Ice 2016
- Speed Weekend on Ice 2018
- Speed Weekend on Ice 2019
- Faktarutor/Guider
- FAQ
- Filmer
- Fordon/projekt
- Media
- Pre season pulsejet 2011
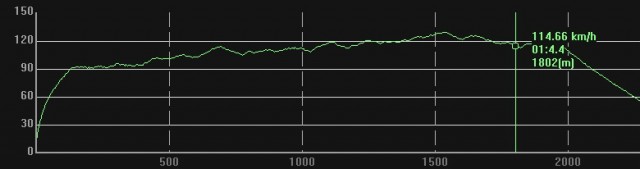
En filmsnutt från andra åket
Publicerat i Filmer, Jetskotern, Speed Weekend on Ice 2013
Lämna en kommentar
Lycka!
Härmed är det första kompletta åket avklarat! Mer rapporter och film kommer senare men vi slänger upp en bild.
Kraft är det ingen brist på i alla fall. Jim tog det väldigt lugnt och tryckte på fullgasknappen ibland. Hastigheten låg ganska jämnt på 120km/h
Publicerat i Allmänt, Jetskotern, Speed Weekend on Ice 2013
4 kommentarer
Nu bär det av!
Publicerat i Speed Weekend on Ice 2013
2 kommentarer
Det är väl som vanligt…
…ju mer nytta vi gör, desto mindre tid har vi till att skriva om det.
Helgen har varit mycket produktiv, och idag gjorde vi den absolut sista provstarten inför Speed Weekend. Vi passade dessutom på att bjuda in de av våra kollegor från Nord-Lock som var intresserade av att se vad fasen vi hade för oss.
Något känns trots allt lite fel. Antagligen för att vi lastat vagnen och gjort klart det mest av packningen två dagar innan avfärd…
Publicerat i Filmer, Jetskotern, Speed Weekend on Ice 2013
1 kommentar
Bränsleförsörjning
Ett komplett pulsjetekipage drivs av två bränslen; bensin och kaffe. Då vi lagt en hel del arbete på det förstnämnda så kände vi att vi även borde se över det andra.
Lustigt nog var det Lars-Erik, som har lägst kaffeförbrukning av oss alla, som tog itu med detta. När två, tre team ska ha kaffe samtidigt duger det inte med någon liten sketen Moccamaster så han krökte ihop en rejäl kaffepanna i rostfritt.
Efter en rejäl sovmorgon och ett par koppar kaffe (ur Moccamastern denna gång) börjar vi planera helgens aktiviteter. Dessa punkter (med flera) ska avklaras:
- Modifiera batterihyllan så att den rymmer de nya batterierna.
- Montera isär och lacka stativet till startfläkten. Den ser för eländig ut…
- Göra klart och montera den nya rostfria strypningsplåten för insuget. Under förra provkörningen, som vi faktiskt inte lagt ut några filmbevis från, gick den gamla aluminiumplåten i tusen bitar.
- Montera skidor samt dragstång på elverket.
- Lite allmänt organiserande och sortering av prylar inför nästa helg.
På tisdag gör vi den sista provstarten innan avfärd, för att kontrollera att allt verkligen funkar efter våra modifieringar.
Mobacken-Anders antydde att de kanske skulle skrämma igång turbinsparken under helgen, så vi väntar tålmodigt på spektakulära filmer från detta.
Publicerat i Allmänt, Jetskotern, Speed Weekend on Ice 2013
3 kommentarer
Spänt var det här!
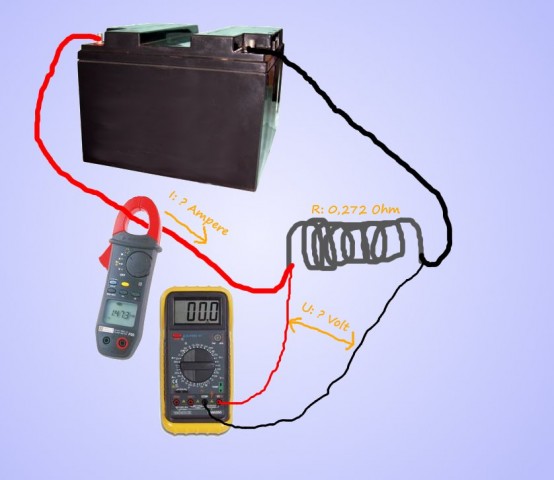
Då vi haft våra misstankar om att det bilbatteri vi använt för att driva bränslepumparna inte varit i högform så tog jag idag och gjorde lite mätningar. Jag hade dessutom fått möjligheten att låna ett par gel-batterier av olika modell, så att jag hade något att jämföra med.
Beväpnad med tångamperemeter (av modellen som även klarar att mäta likström), multimeter och ett kasserat värmeelement från härdanläggningen på Nord-Lock skred jag till verket.
Under vår senaste provkörning tog L-E och mätte hur mycket ström bränslepumparna drog. Han fick till någonting runt 40 A (ampere), vilket är en hel del faktiskt! Tanken var att med värmeelementet belasta batterierna ungefär lika mycket så jag mätte ut två anslutningspunkter på spiralen som gav ungefär 40A ström när den kopplades till batteriet.
Tångamperemetern använde jag för att mäta den ström som gick genom kabeln, och med multimetern mätte jag spänningen över elementet. Detta för att kunna räkna ut dess resistans senare (en vanlig multimeter är inte så bra på att mäta väldigt låga resistanser).
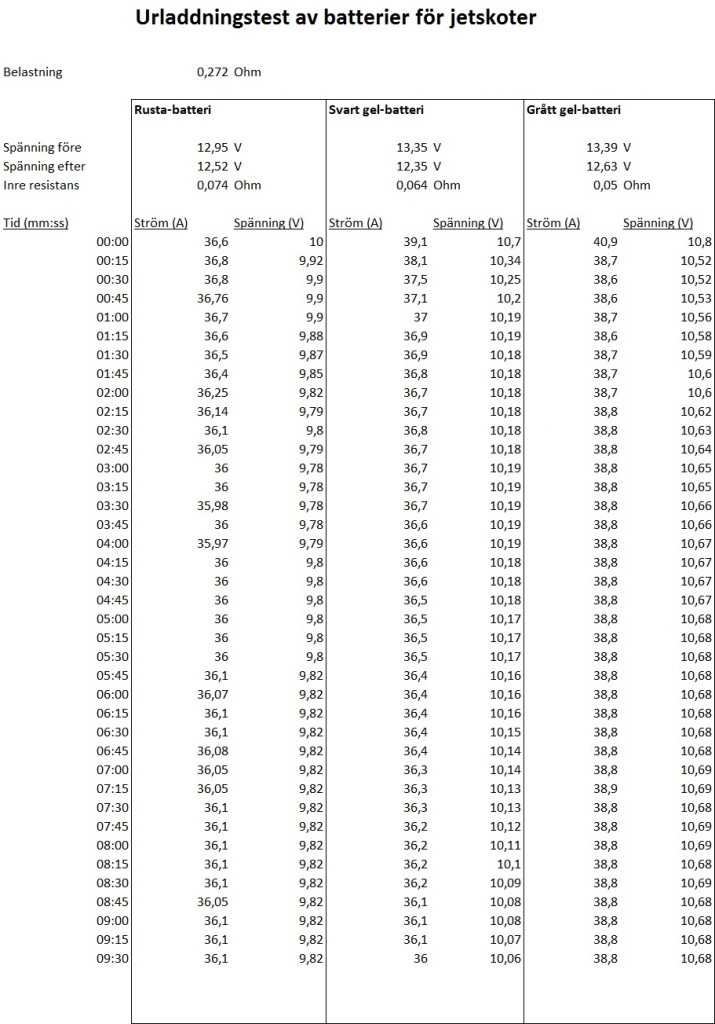
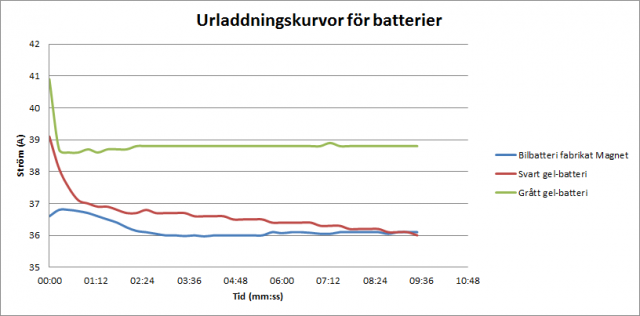
Jag mätte spänningen på varje batteri innan testet och efter utfört test. Under testen så mätte jag spänning och ström med 15 sekunders intervall. Resultaten ser ni i tabellen och grafen nedan.
Det första batteriet jag kollade var det gamla Rustabatteriet (Magnet) som vi kört med sedan tidigare (se den blå grafen). Som ni ser så får man en viss sänkning av strömmen inledningsvis, men sedan lägger den sig på en ganska stabil nivå.
Det andra batteriet var ett svart gel-batteri. Gelbatterierna verkar leverera massor med ström precis efter att man anslutit belastningen, men sedan planar kurvan ut och strömmen lägger sig hyfsat stabilt.
Bäst var det grå gel-batteriet. Inte nog med att det levererade en mycket jämn ström – den var även avsevärt högre än för de andra batterierna.
Inre resistans
I ett perfekt batteri orsakar inte belastningen något spänningsfall. Tyvärr så existerar inte sådana batterier. Den inre resistansen i batteriet gör att utspänningen sjunker när belastningen ökar. Det ser ni tydligt om ni jämför utspänningen vid belastning från tabellen med värdena Spänning före och Spänning efter.
Den spänning som jag skrivit ner i tabellen med mätvärden avser spänningen över värmeelementet. Genom att subtrahera denna från batteriets spänning efter slutfört test (Spänning efter) och dividera med strömmen får jag enligt Ohms lag:
R = U / I = (12,52 – 9,82) / 36,1 = 0,075 Ohm
(Beräknat på de sista mätvärdena från tabellen för Rustabatteriet).
De två andra batterierna gav lägre inre resistans, vilket förstås är bra då de kan leverera mer effekt vid samma belastning.
Kabeldimensioner
Vi har faktiskt inte använt så väldans grova ledningar från batteriet till reläboxarna för bränslepumparna så jag tänkte att jag kanske borde kontrollera förlusterna i dessa. Jag kopplade multimeterns kablar till varsin sida (vid batteriet, samt vid reläboxen) av ena matarkabeln, samt tångamperemetern över samma kabel för att även mäta strömmen.
Sen kopplade jag in värmeelementet vid reläboxen för att simulera pumparnas belastning.
Jag mätte upp ett spänningsfall på 0,45V och en ström på 37,5A. Enligt samma ekvation som ovan ger detta en ledningsresistans på 0,45 / 37,5 = 0,012 Ohm. Vi får också veta att vi bränner bort 0,45 * 37,5 = nästan 17 watt i värme bara i den ena kabeln. Då vi faktiskt har två sådana kablar (en för + och en för -) så blir effektförlusten den dubbla!
Detta duger inte!
Åtgärdsplan
Som ni nu sett, kära läsare, så gjorde det grå gelbatteriet väldigt bra ifrån sig så vi kommer med största sannolikhet att införskaffa minst ett sådant.
Om vi nu skaffade in två sådana batteriet och parallellkopplade dem så skulle vi halvera den totala inre resistansen. Istället för ett spänningsfall på 40 * 0,05 = 2V i batteriet skulle vi få endast en volts spänningsfall. En volt mer ut alltså, och det är knappt 10 procent mer!
Genom att dubbla ledningsarean mellan batteri och reläbox kan vi halvera spänningsfallet även där, så istället för en knapp volt förlorar vi bara knappt en halv volt genom kablarna.
Totalt 1.5 volt mer alltså!
Någon dag till veckan blir det nog en tur till Swedol för inköp av kabel och rejäla förskruvningar. Eftersom Clas Ohlson har valt att fokusera mer på rosa vattenkannor och toalettrullehållare med radio i så får man leta sig till andra ställen. Swedol har nog åkare som en av sina största kundkretsar, och de är nog mer intresserade av rejäla prylar som fungerar än ovan nämnda plastvaror.
Publicerat i Faktarutor/Guider, Jetskotern
7 kommentarer
FAQ: ”Hur många hästkrafter ger den?”
 Under den nya kategorin FAQ (Frequently Asked Questions) tänkte jag att vi kunde besvara några av de frågor som dyker upp oftast.
Under den nya kategorin FAQ (Frequently Asked Questions) tänkte jag att vi kunde besvara några av de frågor som dyker upp oftast.
Jag tror att L-E och Jim håller med om att en av dessa frågor är; ”hur många hästkrafter ger den?”. Jag hoppas verkligen att jag inte strular till det här allt för mycket nu. Faktum är att jag fick dra fram lite gamla böcker från högskoletiden. Jag skäms när jag inser hur mycket jag glömt. Ni förstår säkert att vissa detaljer kan vara utelämnade, bortglömda, dåligt formulerade eller till och med missuppfattade…
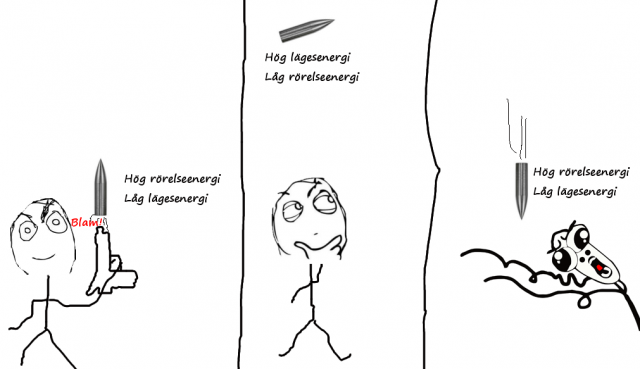
Hästkrafter är ett mått på effekt. Grundenheten för effekt är watt (W), men som med så många andra storheter så kan effekt anges på flera sätt (längdmått kan anges i meter och tum t.ex.).
Effekt beskriver i vilken takt energi omsätts från en form till en annan. Som vi lärde oss i grundskolefysiken så kan energi existera i olika former, t.ex värme-, läges- och rörelseenergi (kinetisk energi).
Ett exempel
En gevärskula som skjuts rakt uppåt har, när den lämnar pipan, hög hastighet, och följaktligen hög rörelseenergi. Ju längre upp den kommer desto långsammare färdas den. Lägesenergin ökar med höjden och rörelseenergin avtar. Alltså omvandlas rörelseenergi till lägesenergi.
Till slut har all rörelseenergi övergått till lägesenergi (faktiskt även en del värme pga friktionen mot luften), och tyngdkraften tar över. Kulan accelererar åter igen. Lägesenergin avtar, rörelseenergin ökar.
När kulan träffar marken omvandlas den rörelseenergi den fortfarande har till värme vid träffen.
Arbete
Effekt kan också beskrivas som ett mått på hur mycket arbete som utförs på en viss tid. Att lyfta ett klot en meter kräver lika mycket energi (arbete) oavsett hur kort tid man gör det på. Dock krävs det dubbelt så mycket effekt för att göra det på hälften så lång tid.
Effekten i en bilmotor
När man anger effekten på en bilmotor så avser man den maximala effekt som man kan få ut från motorns vevaxel. Man anger alltså i vilken hastighet motorn kan omvandla kemisk energi (bränslet) till rörelseenergi (som alla vet så avger bilmotorn även en hel del värme, och den effekten tar man inte hänsyn till).
Genom att transportera ner kraften från vevaxeln till marken genom växellådan och däcken kan man öka hastigheten på bilen.
Det som i slutändan bestämmer bilens maxhastighet är luftmotståndet och markfriktionen. Motorns effekt måste räcka för att övervinna dessa två för att hastigheten ska fortsätta öka. När hastigheten inte längre ökar så innebär det att all rörelseenergi från vevaxeln omvandlas till värmeenergi genom friktionen.
Förhållandet mellan kraft (F), hastighet (v) och effekt (P) är som följer:
P = F * v
Ponera att vi har en bil vars motor ger 100 hästkrafter (~74570 watt) och att den har en maxhastighet på 200 km/h (~55.6 m/s). Den kraft som luftmotstånd och markfriktion ger upphov till är då
F = P / v = 74570 / 55.6 = ~1341 N (Newton).
I en bil kan man ha ett ganska konstant effektuttag, då man vid låg hastighet (låg växel) har en hög dragkraft och vid hög hastighet (hög växel) har en låg dragkraft.
Hur är det med pulsjeten då?
Framdrivningen med en jetmotor fungerar inte likadant som med en bilmotor. Istället för att föra över kraft via hjulen så skapar jetmotorn drivkraft genom att accelerera materia.
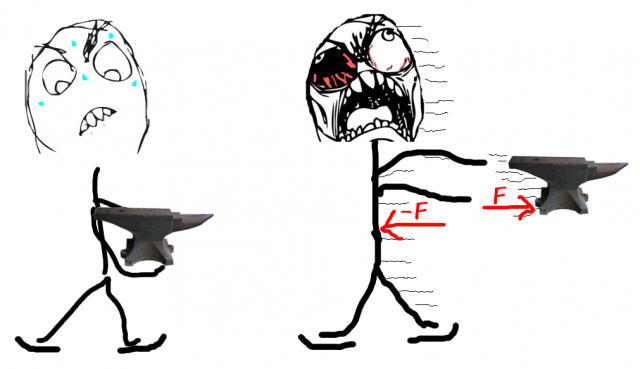
Tänk er att ni av någon anledning tagit med er ett städ ut på en skridskobana. Av någon ännu mer outgrundlig anledning vill ni nu kasta städet så långt som möjligt, d.v.s accelerera dess hastighet så att det flyger iväg.
Ni märker ganska omgående att det inte är bara städet som får fart – utan även ni, fast i motsatt riktning.
Den kraft som anbringas på städet resulterar i en precis lika stor kraft på er, vilket får även er att accelerera. Det är denna kraft som man i jetmotorer kallar för dragkraft.
I en pulsjet skapas denna kraft av de gaser som expanderar kraftigt under explosionsfasen i varje puls. Kraften varierar i samma takt som pulserna så den dragkraft vi angivit efter våra provkörningar kan ses som ett medelvärde av dessa variationer.
Kan vi räkna ut effekten från pulsjetmotorn?
Enligt formeln ovan så får vi effekten genom att multiplicera hastighet med dragkraft. Den dragkraft vi uppmätt vid stillestånd ligger någonstans runt 1700 N. Låt säga att vi skulle nå en maxhastighet på 200 km/h (~55.6 m/s) så får vi då alltså en effekt på:
P = 55.6 * 1700 = 94444 watt = ~126.7 hästkrafter.
Inte så imponerande egentligen om man tar hänsyn till den enorma mängd bensin som går åt…
Till skillnad från bilen där man genom att välja växel kan öka dragkraften vid låg fart så går inte detta på pulsjeten. Därför blir effekten proportionerlig mot hastigheten. Ju högre hastighet, desto högre effekt. Därför har också ett jetdrivet fordon relativt låg acceleration vid låg hastighet.
Faktum kvarstår: Pulsjetmotorer är vansinnigt ineffektiva när det gäller att omvandla kemisk energi till rörelseenergi…
Värmeeffekt då?
Pga motorns låga effektivitet omvandlas så gott som all energi till värme redan i motorn. Resterande energi omvandlas till värme genom friktionen mot luften och marken så snart man nått topphastighet.
Energiinnehållet i bensin ligger på runt 34,8 MJ (Megajoule) per liter och motorn drar någonstans runt 12 liter per minut. Detta ger en effekt på 34,8 * 12 / 60 = 6,96 MJ/s = 6.96 Megawatt. Ja ni läste rätt. Megawatt! Inte undra på att man tycker det blir lite småvarmt när man står och torrkör maskineriet ute på gården.
Säg att en villa har ett effektbehov på 5kW. Med värmeeffekten ovan skulle vi kunna värma närmare 1400 villor. Inte undra på att de trodde att vi höll på med något fjärrvärmeverk när vi beställde oljemunstycken!
Verkningsgrad
Den värme som utvecklas i motorn är ju ganska icke önskvärd när det främsta syftet med en jetmotor är att driva ett fordon framåt. Man brukar använda ordet verkningsgrad för att beskriva hur stor del av den förbrukade energin som faktiskt åtgår till det tänkta ändamålet. Alla siffror ovan är ju högst godtyckliga, men det bör i alla fall gå att få någon slags uppfattning om effektiviteten på en pulsjet:
Total energi per sekund: 69600000 J
Energi som ger maskinen fart: 94444 J
Verkningsgrad = 94444/69600000 = 0,0136 = 1,36 %
Disclaimer
Ta inte allt för allvarligt på dessa värden nu. Det enda vi kan kalla för ”fakta” är det vi faktiskt mätt upp i verkligheten, d.v.s. dragkraften. Topphastigheten hoppas vi att få kontrollera en gång för alla under Speed Weekend och bränsleförbrukningen borde vi mäta noggrannt så att vi faktiskt har något mer än ett teoretiskt värde.
En gammal mattelärare sade att så länge man ligger inom rätt tiopotens så har man lyckats skapligt. Tror att vi ska hålla oss inom det i alla fall.
Nu är frågan hur vi sammanfattar detta i max två meningar så att vi har något snabbt svar när denna fråga dyker upp gång på gång i Orsa…
Dagen efter;
Kort svar
Den teoretiska effekten känner vi inte till förrän vi vet hur fort maskinen går, då den beräknas från dragkraft och hastighet.
På grund av motorns oerhört låga verkningsgrad lär inte beräknad effekt vara lika imponerande som ljudet.
Publicerat i Faktarutor/Guider, FAQ
4 kommentarer
Dragkraft och hastighet
Det finns en helt fantastisk rapport kallad Sea-level performance tests of a 22-inch-diameter pulse-jet engine at various simulated ram pressures att ladda ner från NASAs hemsida; Länk.
Någon gång under eller efter andra världskrigets slut så kom amerikanerna över en av tyskarnas V1:or. Antagligen var det inte så svårt eftersom de slagit ner lite här och var (många träffade inte alls det tänka målet). De byggde en replika av denna och utförde en rad avancerade tester. Antagligen var de intresserade av att nyttja tekniken själva.
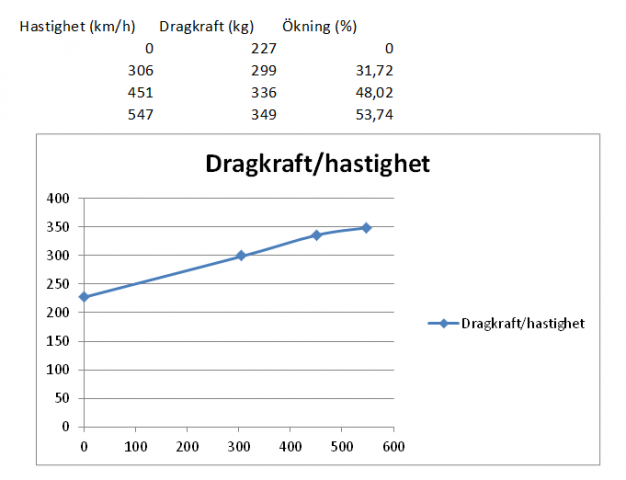
Deras motor var en aning större och gav ungefär 220-230 kg dragkraft vid stillestånd. Här nedanför ser man ett utdrag ur rapporten där man ser att dragkraften ökar rejält vid riktigt höga hastigheter.
Vi översätter till mått som vi förstår:
En rejäl ökning!
Värt att notera är att det är väldigt höga hastigheter det handlar om i grafen ovan, men om man genar lite och approximerar ökningen vid 150 knyck till 10-15% så har vi i alla fall minst 20kg till att leka med.
Väldans praktiskt med ökande dragkraft vid ökande hastighet och luftmotstånd. Som tur är så ökar luftmotståndet snabbare…
Publicerat i Faktarutor/Guider, Jetskotern
6 kommentarer
Så här sätter man ihop ventilpaketet
Ventilpaketet är en av de delar på pulsjeten som vi har lagt mest energi på, både vid konstruktion och tillverkning.
Det består av 17 CNC-frästa ventil-/ändblock, laserskurna packningar, närmare 300 härdade styrpinnar och 180 klippta, böjda, trådgnistade och värmebehandlade ventiler av rostfritt stål.
Filmklippet visar hur man monterar ihop det hela.
Publicerat i Filmer, Jetskotern
4 kommentarer
Dragkraft, luftmotstånd och acceleration
Med risk för att bli oerhört tråkig eller framstå som en besserwisser för många tänkte jag redogöra lite om mina senaste klurerier (jodå, vi klurar väldigt mycket allihopa men det är väl jag som gillar bäst att pracka på andra det som rör sig i mitt huvud)…
Att i förväg räkna på saker kan både vara intressant och/eller helt nödvändigt. I detta fallet är det kanske mest av rent intresse jag ansträngt hjärncellerna lite.
Newtons andra rörelselag ger oss ett förhållande mellan ett föremåls (med känd massa) acceleration och den kraft som påverkar detta:
F = m * a
Den kraft som påverkar föremålet betecknas F och mäts i Newton (N). Föremålets massa (m) mäts i kilo och accelerationen mäts i m/s^2 (”meter per sekundkvadrat”).
Det sista (m/s^2) kan se lite lustigt ut för den oinvigde men går enkelt att tolka som ”meter per sekund, per sekund”, d.v.s hur mycket föremålets hastighet (i m/s) ökar per sekund. Hmm, det där kanske bara blev rörigt.
Om vi för skojs skull ska försöka tillämpa detta på vår fina pulsjetmaskin…
Massan känner vi till då vi mätte den i höstas med den fina nyinköpta lastcellen. Massan uppgår till ~300kg. Med chaufför och lite mer soppa i tankarna får vi räkna med 400kg.
Kraften F i ekvationen ovan utgörs faktiskt av summan av alla krafter som påverkar jetskotern. De tre betydande krafterna är motorns dragkraft, markfriktionen och luftmotståndet. Krafter så som hemlängtan och full blåsa verkar mest betydande vid hastighetsmätning på trimmade Puchar så vi bortser från dem.
Markfriktionen är väldigt låg, men jag garderar mig och höftar till med att det krävs 98,2N (10kg * 9.82) för att hålla jetskotern i rörelse över isen.
Luftmotståndet känner vi inte till. Detta varierar förstås också med hastigheten. För tillfället sätter jag det till noll.
Motorns dragkraft har vi mätt upp till runt 1700N.
Summan av krafterna som påverkar jetskotern blir då:
1700N – 100N = 1600N.
Vi har alltså nu:
F = 1600N
m = 400kg
Den fina formeln ovan ger oss då:
a = F / m –> a = 1600 / 400 = 4 m/s^2.
4 meterpersekundkvadrat säger oss alltså att hastigheten ökar med 4m/s i sekunden.
Efter 10 sekunder bör vi alltså ha en hastighet på 40m/s, vilket är 144km/h.
Ja, du tänkte rätt: Detta stämmer inte. Luftmotståndet blir ganska betydande när hastigheten ökar, och det kommer antagligen att gå rätt mycket långsammare efter 10 sekunder. Det roliga i det här är att när vi väl fått in en logg från första repan kan vi räkna ut det verkliga luftmotståndet då detta är den enda okända parametern (av större betydelse) i ekvationerna ovan.
Förra året gjorde jag dessa beräkningar ”baklänges” för att från hastighetsloggen från (den enda) repan på långbanan räkna ut dragkraften. Detta var innan vi hade gjort någon riktig mätning. Det roliga var att det stämde rätt bra.
Såna här finfina mätare som man kan sätta i bilen, som uppskattar motoreffekten medan man kör en repa fungerar på ett liknande sätt. De mäter accelerationen, och man knappar in bilens vikt. Utifrån detta (och säkerligen några fler parametrar) räknar den ut resten. Matematik är faktiskt väldigt kul ibland!
(Undrar hur många läsare vi tappat nu…)
Publicerat i Faktarutor/Guider
5 kommentarer